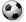4x2+1
___________ + 1- 5x
_______
(x+1)(x-3) x-3
mogł by mi ktoś z was powiedizeć jak to sie robi i rozwiac chodziasz ten jeden przyklad dla wzoru pozostalłe juz sobie zrobie sam
lista tematów
Matematyka-wyrazenia wymierne - prosze o pomoc!
Konto usunięte: mogł by mi ktoś z was powiedizeć jak to sie robi i rozwiac chodziasz ten jeden przyklad dla wzoru pozostalłe juz sobie zrobie sam
a większymi nie mogłeś, prawda?

ale jakie jest polecenie?
i ten zapis ma się do czego? że niby co?
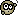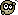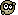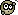
4x2+1
___________ + 1- 5x
_______
(x+1)(x-3) x-3
to 2 ułamki są tak to ma wygladac?? a polecenie jest wykonaj działania a wynik podaj w najprostrzej postaci!
___________ + 1- 5x
_______
(x+1)(x-3) x-3
to 2 ułamki są tak to ma wygladac?? a polecenie jest wykonaj działania a wynik podaj w najprostrzej postaci!
4x2+1
___________ + 1- 5x
(x+1)(x-3)( x-3)
Czy to miało być tak?
Lepiej zapisuj inaczej : P W(x)=(4x^2+1)/[(x+1)(x-3)(x -3)] + 1-5x
1.
Musisz sprowadzić wszystko do jednego ułamka (mnożymy 1-5x przez czyli 1 ([(x+1)(x-3)x -3]/[(x+1)(x-3)(x -3)] po to aby uzyskać taki sam mianownik
W(x)=(4x^2+1 )/ [(x+1)(x-3)(x -3)] + (1-5x) *[(x+1)(x-3)(x -3)] / [(x+1)(x-3)(x -3)]
2.
Funkcje przyrównujemy do zera, aby znaleźć x ( punkty w którym funkcja przecina sie z osia pozioma x)
(4x^2+1 )/ [(x+1)(x-3)(x -3)] + (1-5x) *[(x+1)(x-3)(x -3)] / [(x+1)(x-3)(x -3)] = 0
Dla ułatwienia obliczeń podstawiamy za mianownik V(x), a za licznik G(x)
Czyli nasz wielomian W(x)=(4x^2+1 )/ [(x+1)(x-3)(x -3)] + (1-5x) *[(x+1)(x-3)(x -3)] / [(x+1)(x-3)(x -3)]
Gdzie:
V(x) = (4x^2+1 ) + (1-5x) *[(x+1)(x-3)(x -3)]
a
G(x) = [(x+1)(x-3)(x -)3]
3. Ustalanie dziedziny funkcji czyli: ustalanie "miejsca" gdzie funkcji po prostu nie moze byc a potem wyrzuceniu tych wynikow ze zbioru. Wynika to z niekotrych zaleznosci matematycznych tj.
W mianowniku nie może być 0 !
-Pod pierwiastkiem stopni parzystych 2,4,6,8.. nie może być liczby ujemnej, pamiętaj jednak ze może być liczba ujemna przy pierwiastkami stopni nieparzystych np 3,5.
-Podstawa logarytmu musi być większa od zera i rożna od jeden oraz liczba logarytmowana powinna być większa od 0
W naszym przypadku pod kreska ułamkowa nie może być 0, wiec G(x)!=0 (!= zapis ten oznacza, ze G(x) musi być rozny od 0).
G(x)=[(x+1)(x-3)(x-3)] != 0 ... wyszukujemy przeciec funkcji G(x) z osi-a x-ow)
czyli x+1 = 0, x-3= 0, x-3=0
x=-1, x=3, x=3 (x=3 jest pierwiastkiem podwójnym)
Wszystkie te punkty nie mogą byc równe zero, wiec nie beda one należały do dziedziny W(x), wiec zapisujemy W(x) : D E R/ { 1,3 };
W przypadku nierówności typu > < sprawa jest trochę trudniejsza ( jak by co to priv )
4. Wyliczasz przeciecia z osia X ale tym razme funkci nad kreska ulamkowa. V(x)
(4x^2+1 ) + (1-5x) *[(x+1)(x-3)(x -3)]=0
4x^2+1 + ... wymnóż wszystko ze sobą pododawaj i znajdź x-y dla V(x) = 0
Znalezione x-wy wypisz sobie i sprawdź czy zawierają się z zbiorze spod punktu 3ciego, jeżeli jakiś x nie należy do dziedziny rozwiązań to go po prostu nie pisz : )
Nie będę tego rozwiązywał bo sam mam sporo do zrobienia. Mam nadzieje, ze w miarę logicznie wytłumaczyłem od czego zacząć rozwiązywanie takich głupot : )
___________ + 1- 5x
(x+1)(x-3)( x-3)
Czy to miało być tak?
Lepiej zapisuj inaczej : P W(x)=(4x^2+1)/[(x+1)(x-3)(x -3)] + 1-5x
1.
Musisz sprowadzić wszystko do jednego ułamka (mnożymy 1-5x przez czyli 1 ([(x+1)(x-3)x -3]/[(x+1)(x-3)(x -3)] po to aby uzyskać taki sam mianownik
W(x)=(4x^2+1 )/ [(x+1)(x-3)(x -3)] + (1-5x) *[(x+1)(x-3)(x -3)] / [(x+1)(x-3)(x -3)]
2.
Funkcje przyrównujemy do zera, aby znaleźć x ( punkty w którym funkcja przecina sie z osia pozioma x)
(4x^2+1 )/ [(x+1)(x-3)(x -3)] + (1-5x) *[(x+1)(x-3)(x -3)] / [(x+1)(x-3)(x -3)] = 0
Dla ułatwienia obliczeń podstawiamy za mianownik V(x), a za licznik G(x)
Czyli nasz wielomian W(x)=(4x^2+1 )/ [(x+1)(x-3)(x -3)] + (1-5x) *[(x+1)(x-3)(x -3)] / [(x+1)(x-3)(x -3)]
Gdzie:
V(x) = (4x^2+1 ) + (1-5x) *[(x+1)(x-3)(x -3)]
a
G(x) = [(x+1)(x-3)(x -)3]
3. Ustalanie dziedziny funkcji czyli: ustalanie "miejsca" gdzie funkcji po prostu nie moze byc a potem wyrzuceniu tych wynikow ze zbioru. Wynika to z niekotrych zaleznosci matematycznych tj.
W mianowniku nie może być 0 !
-Pod pierwiastkiem stopni parzystych 2,4,6,8.. nie może być liczby ujemnej, pamiętaj jednak ze może być liczba ujemna przy pierwiastkami stopni nieparzystych np 3,5.
-Podstawa logarytmu musi być większa od zera i rożna od jeden oraz liczba logarytmowana powinna być większa od 0
W naszym przypadku pod kreska ułamkowa nie może być 0, wiec G(x)!=0 (!= zapis ten oznacza, ze G(x) musi być rozny od 0).
G(x)=[(x+1)(x-3)(x-3)] != 0 ... wyszukujemy przeciec funkcji G(x) z osi-a x-ow)
czyli x+1 = 0, x-3= 0, x-3=0
x=-1, x=3, x=3 (x=3 jest pierwiastkiem podwójnym)
Wszystkie te punkty nie mogą byc równe zero, wiec nie beda one należały do dziedziny W(x), wiec zapisujemy W(x) : D E R/ { 1,3 };
W przypadku nierówności typu > < sprawa jest trochę trudniejsza ( jak by co to priv )
4. Wyliczasz przeciecia z osia X ale tym razme funkci nad kreska ulamkowa. V(x)
(4x^2+1 ) + (1-5x) *[(x+1)(x-3)(x -3)]=0
4x^2+1 + ... wymnóż wszystko ze sobą pododawaj i znajdź x-y dla V(x) = 0
Znalezione x-wy wypisz sobie i sprawdź czy zawierają się z zbiorze spod punktu 3ciego, jeżeli jakiś x nie należy do dziedziny rozwiązań to go po prostu nie pisz : )
Nie będę tego rozwiązywał bo sam mam sporo do zrobienia. Mam nadzieje, ze w miarę logicznie wytłumaczyłem od czego zacząć rozwiązywanie takich głupot : )