Konto usunięte: Nie wiem też czy sie przypadkiem w czymś nie pogubiłem...
Pogubiłeś się już na samym początku, te stożki nie są takie same, mają różne wysokości...
Bryła po "spłaszczeniu" będzie deltoidem.
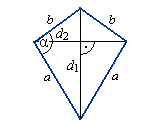
P= a*b*sinα
P = 1/2 d1*d2
z tego można wyznaczyć promień okręgu, a później przy pomocy tw. Pitagorasa wysokości stożków.