Funkcje trygonometryczne

sinusoida – wykres funkcji $y=\sin x$

kosinusoida – wykres funkcji $y=\cos x$

tangensoida – wykres funkcji $y=\operatorname {tg} x$

Leonhard Euler (1707–1783) – szwajcarski matematyk, który udowodnił pewne własności funkcji trygonometrycznych, m.in. ich związek z funkcją wykładniczą nazywany wzorem Eulera.

Funkcje trygonometryczne – funkcje matematyczne wyrażające między innymi stosunki długości boków trójkąta prostokątnego zależnie od miary jego kątów wewnętrznych. Funkcje te wywodzą się z geometrii, ale są rozpatrywane także w oderwaniu od niej, dla argumentów rzeczywistych i zespolonych. Uogólnienie funkcji dokonywane jest w analizie matematycznej, w której opisano je szeregami potęgowymi. Powstały też inne definicje, oparte np. na równaniach różniczkowych, równaniach funkcyjnych, iloczynach nieskończonych oraz ułamkach łańcuchowych.

Pojęcie funkcji trygonometrycznych jako pierwszy wprowadził Euler, zanim to nastąpiło matematycy uważali wartości trygonometryczne jako linie ciągłe połączone za pomocą okręgu.

Do funkcji trygonometrycznych zalicza się przede wszystkim sinus, kosinus i tangens, a także kotangens, sekans, kosekans i kilka innych, wspominanych rzadziej. Funkcje trygonometryczne to główny przedmiot badań trygonometrii; jej dział poświęcony tym funkcjom nazywano goniometrią, przy czym termin ten ma też inne znaczenia. Badania te rozpoczęto w starożytności, a konkretniej starożytnej Grecji, po czym rozwijali ją uczeni indyjscy, islamscy i ze średniowiecznej Europy. W czasach nowożytnych podano dla tych funkcji:

• rozwinięcia w szeregi potęgowe,
• uogólnienia na argumenty zespolone,
• związki z funkcją wykładniczą takie jak wzór Eulera,
• rozwinięcia w iloczyny nieskończone.

Na przestrzeni stuleci podano też dziesiątki tożsamości trygonometrycznych, które m.in. wiążą te funkcje ze sobą. Funkcje trygonometryczne zalicza się do elementarnych i stosuje w różnych działach matematyki jak geometria, analiza i teoria liczb. Korzystają z nich nauki ścisłe – zarówno przyrodnicze, społeczne, jak i techniczne. Jednym z powodów jest to, że funkcjami sinus i kosinus można modelować zjawiska okresowe jak drgania mechaniczne.

Definicje

Istnieje kilka definicji funkcji trygonometrycznych, bazujących zarówno na pojęciach geometrycznych, jak i analitycznych.

Przez trójkąt prostokątny

Oznaczenia boków i kątów trójkąta prostokątnego użyte w definicji

Funkcje trygonometryczne danego kąta ostrego w trójkącie prostokątnym definiuje się jako stosunek długości odpowiednich dwóch boków tego trójkąta:

funkcja	polskie oznaczenie	definicje
		przez boki – stosunek długości	przez inne funnkcje
sinus	$\sin$	przyprostokątnej $a$ leżącej naprzeciw kąta $\alpha$ i przeciwprostokątnej $c$
kosinus	$\cos$	przyprostokątnej $b$ przyległej do kąta $\alpha$ i przeciwprostokątnej $c$
tangens	$\operatorname {tg}$	przyprostokątnej $a$ leżącej naprzeciw kąta $\alpha$ i przyprostokątnej $b$ przyległej do tego kąta
kotangens	$\operatorname {ctg}$	przyprostokątnej $b$ przyległej do kąta $\alpha$ i przyprostokątnej $a$ leżącej naprzeciw tego kąta	${\tfrac {1}{\operatorname {tg} }}$
sekans	$\sec$	przeciwprostokątnej $c$ i przyprostokątnej $b$ przyległej do kąta $\alpha$	odwrotność kosinusa $({\tfrac {1}{\cos }})$
kosekans	$\operatorname {cosec}$	przeciwprostokątnej $c$ i przyprostokątnej $a$ leżącej naprzeciw kąta $\alpha$	odwrotność sinusa $({\tfrac {1}{\sin }})$

Powyższe definicje można zebrać w postaci tabelki:

	${\tfrac {a}{\cdot }}$	${\tfrac {b}{\cdot }}$	${\tfrac {c}{\cdot }}$
${\tfrac {\cdot }{a}}$	$1$	$\operatorname {ctg} \alpha$	$\operatorname {cosec} \alpha$
${\tfrac {\cdot }{b}}$	$\operatorname {tg} \alpha$	$1$	$\sec \alpha$
${\tfrac {\cdot }{c}}$	$\sin \alpha$	$\cos \alpha$	$1$

Do tej listy włączano też kilka innych funkcji; haversin upraszcza obliczanie odległości punktów na powierzchni Ziemi:

funkcja	symbol i definicja
sinus versus	$\operatorname {versin} \alpha =1-\cos \alpha$
haversin (ang. half of the versine)	$\operatorname {haversin} \alpha ={\tfrac {1}{2}}\operatorname {versin} \alpha$
cosinus versus	$\operatorname {covers} \alpha =1-\sin \alpha$
exsecans	$\operatorname {exsec} \alpha =\sec \alpha -1$

Przez okrąg jednostkowy i etymologia nazw

Definicja na okręgu jednostkowym

Jeżeli wokół wierzchołka kąta poprowadzony zostanie okrąg o promieniu 1, czyli tzw. okrąg jednostkowy, to funkcje trygonometryczne miary kąta ostrego $\theta$ wyrażać się będą przez długości odpowiednich odcinków:

$\sin \theta =|AC|$

$\cos \theta =|OC|$

$\operatorname {tg} \theta =|AE|$

$\operatorname {ctg} \theta =|AF|$

$\sec \theta =|OE|$

$\operatorname {cosec} \theta =|OF|$

Alternatywnie, jako argument funkcji trygonometrycznych zamiast długości łuku $DA$ można przyjąć pole wycinka $OBDA$ – ich wartości dla promienia 1 są równe. Definicja na okręgu jednostkowym ma swój odpowiednik dla funkcji hiperbolicznych, gdzie argument funkcji definiowany jest jako pole wycinka hiperboli, analogicznego do $OBDA$.

Definicja ta była historycznie pierwsza. Wynikają z niej nazwy funkcji trygonometrycznych. Pierwotnie tymi nazwami określano właśnie długości odpowiednich odcinków, niekoniecznie na okręgu jednostkowym.

• Sinus, czyli połowa długości cięciwy $AB,$ był w pracach hinduskiego matematyka Aryabhaty w sanskrycie nazywany ardha-jiva („połowa cięciwy”), co zostało skrócone do jiva, a następnie transliterowane do arabskiego jiba (جب). Europejscy tłumacze, Robert z Chester i Gerardo z Cremony w XII-wiecznym Toledo pomylili jiba z jaib (جب), oznaczającym „zatokę” prawdopodobnie dlatego, że jiba (جب) i jaib (جب) są tak samo pisane po arabsku (informacja o samogłoskach jest gubiona w piśmie). Sinus znaczy po łacinie właśnie zatoka.
• Tangens pochodzi od łacińskiego tangere – dotykający, styczny, gdyż odcinek $AE$ jest styczny do okręgu.
• Secans pochodzi z łacińskiego secare – dzielić, rozcinać, rozstrzygać i znaczy odcięcie. Pierwotnie nazwa odnosiła się do odcinka $OE,$ odcinanego przez styczną (tangens).
• Cosinus, cotangens i cosecans powstały przez złożenie łacińskiego co- (wspólnik, towarzysz) i słów sinus, tangens i secans. Pierwotnie cosinus był nazywany complementi sinus, czyli sinus kąta dopełniającego. Rzeczywiście jest on równy sinusowi miary kąta dopełniającego $\angle AOF.$ Podobnie cotangens i cosecans są równe tangensowi i secansowi tego kąta. Przedrostek „ko-” był jednak używany w stosunku do cosinusa już w sanskrycie u Aryabhaty (koti-jya, kojya); trudno określić, w jakim stopniu nazwa łacińska do tego nawiązuje.

Przez szereg Taylora

Funkcja sinus i jej aproksymacje wielomianami stopnia 1, 3, 5, 7, 9, 11 i 13 utworzonymi z początkowych wyrazów szeregu Taylora

Definicje za pomocą szeregów Taylora określają wartości funkcji trygonometrycznych dla dowolnych liczb rzeczywistych, dla których da się je zdefiniować, pozwalają też na uogólnienie tych funkcji na zbiór liczb zespolonych, kwaternionów, macierzy, a nawet na algebry operatorów, przestrzenie unormowane czy pierścienie nilpotentne. Definicje te są stosowane do numerycznego obliczania wartości funkcji trygonometrycznych.

Zachodzą równości:

${\begin{aligned}\sin x&=x-{\tfrac {x^{3}}{3!}}+{\tfrac {x^{5}}{5!}}-{\tfrac {x^{7}}{7!}}+\ldots =\\&=\sum _{n=0}^{\infty }(-1)^{n}{\tfrac {x^{2n+1}}{(2n+1)!}},\\\cos x&=1-{\tfrac {x^{2}}{2!}}+{\tfrac {x^{4}}{4!}}-{\tfrac {x^{6}}{6!}}+\ldots =\\&=\sum _{n=0}^{\infty }(-1)^{n}{\tfrac {x^{2n}}{(2n)!}},\\\operatorname {tg} x&=x+{\tfrac {x^{3}}{3}}+{\tfrac {2x^{5}}{15}}+\ldots =\\&=\sum _{n=1}^{\infty }{\tfrac {B_{2n}(-4)^{n}(1-4^{n})}{(2n)!}}x^{2n-1},\quad |x|<{\tfrac {\pi }{2}},\end{aligned}}$

gdzie $B_{n}$ to liczby Bernoulliego,

${\begin{aligned}\operatorname {ctg} x&={\tfrac {1}{x}}-{\tfrac {x}{3}}-{\tfrac {x^{3}}{45}}-{\tfrac {2x^{5}}{945}}-\ldots =\\&=\sum _{n=0}^{\infty }{\tfrac {(-1)^{n}2^{2n}B_{2n}x^{2n-1}}{(2n)!}},\quad 0<|x|<\pi ,\\\sec x&=1+{\tfrac {x^{2}}{2}}+{\tfrac {5x^{4}}{24}}+{\tfrac {61x^{6}}{720}}+\ldots =\\&=\sum _{n=0}^{\infty }{\tfrac {(-1)^{n}E_{2n}}{(2n)!}}x^{2n},\quad |x|<{\tfrac {\pi }{2}},\end{aligned}}$

gdzie $E_{n}$ to liczby Eulera,

${\begin{aligned}\operatorname {cosec} x&={\tfrac {1}{x}}+{\tfrac {x}{6}}+{\tfrac {7x^{3}}{360}}+{\tfrac {31x^{5}}{15120}}+\ldots =\\&=\sum _{n=0}^{\infty }{\tfrac {(-1)^{n+1}2(2^{2n-1}-1)B_{2n}x^{2n-1}}{(2n)!}},\quad 0<|x|<\pi .\end{aligned}}$

Każdą z funkcji trygonometrycznych, na dowolnym przedziale zawierającym się w jej dziedzinie, można z dowolną dokładnością jednostajnie przybliżać wielomianami. W otoczeniu zera mogą do tego służyć początkowe wyrazy szeregu Taylora. Nie jest jednak możliwe jednostajne przybliżenie wielomianami funkcji trygonometrycznych w całej ich dziedzinie, jeśli dziedzina przybliżanej funkcji nie jest zbiorem liczb rzeczywistych $\mathbb {R} .$

Przez równania funkcyjne

Twierdzenie: Istnieje dokładnie jedna para funkcji rzeczywistych $(s,c)$ taka, że dla każdego $x,y\in \mathbb {R} {:}$

${\begin{cases}s(x)^{2}+c(x)^{2}=1\\[2pt]s(x+y)=s(x)c(y)+c(x)s(y)\\[2pt]c(x+y)=c(x)c(y)-s(x)s(y)\\[2pt]0<xc(x)<s(x)<x\ \mathrm {dla} \ 0<x<1\end{cases}}$

Tymi funkcjami są:

$s(x)=\sin x,\quad c(x)=\cos x.$

Funkcje trygonometryczne sinus i cosinus można zdefiniować również jako jedyne funkcje $s(x)$ oraz $c(x)$ spełniające poniższe trzy warunki:

${\begin{cases}s(x_{1}-x_{2})=s(x_{1})c(x_{2})-c(x_{1})s(x_{2})\\[2pt]c(x_{1}-x_{2})=c(x_{1})c(x_{2})+s(x_{1})s(x_{2})\\[2pt]\lim _{x\to 0}{\tfrac {s(x)}{x}}=1\end{cases}}$

Przez równania różniczkowe

Sinus i cosinus są rozwiązaniami szczególnymi równania różniczkowego

$y''=-y,$

które opisuje m.in. ruch masy podwieszonej na sprężynie (tzw. oscylator harmoniczny, patrz Harmoniki).

Sinus jest jedynym rozwiązaniem tego równania spełniającym warunki:

${\begin{cases}y(0)=0\\[2pt]y\,'(0)=1\end{cases}}$

Cosinus natomiast jest jedynym rozwiązaniem, dla którego

${\begin{cases}y(0)=1\\[2pt]y\,'(0)=0\end{cases}}$

Przez iloczyny nieskończone

Funkcje trygonometryczne można też wprowadzić za pomocą iloczynów nieskończonych:

$\sin x=x\prod _{n=1}^{\infty }\left(1-{\tfrac {x^{2}}{\pi ^{2}n^{2}}}\right),$

$\cos x=\prod _{n=1}^{\infty }\left(1-{\tfrac {x^{2}}{\pi ^{2}(n-{\frac {1}{2}})^{2}}}\right).$

Przez ułamki łańcuchowe

Niektóre funkcje trygonometryczne można wyrazić w postaci ułamków łańcuchowych:

$\sin x={\cfrac {x}{1+{\cfrac {x^{2}}{(2\cdot 3-x^{2})+{\cfrac {2\cdot 3x^{2}}{(4\cdot 5-x^{2})+{\cfrac {4\cdot 5x^{2}}{(6\cdot 7-x^{2})+\ldots }}}}}}}},$

$\operatorname {tg} x={\cfrac {x}{1-{\cfrac {x^{2}}{3-{\cfrac {x^{2}}{5-{\cfrac {x^{2}}{7-\ldots }}}}}}}}={\cfrac {1}{{\cfrac {1}{x}}-{\cfrac {1}{{\cfrac {3}{x}}-{\cfrac {1}{{\cfrac {5}{x}}-{\cfrac {1}{{\cfrac {7}{x}}-\ldots }}}}}}}},$

$\operatorname {ctg} x={\cfrac {1}{x}}-{\cfrac {x}{3-{\cfrac {x^{2}}{5-{\cfrac {x^{2}}{7-{\cfrac {x^{2}}{9-\ldots }}}}}}}}$

Przez ogólniejsze funkcje

Funkcje trygonometryczne można też zdefiniować analitycznie jako szczególne przypadki funkcji Bessela, funkcji Mathieu albo funkcji eliptycznych Jacobiego.

Własności w dziedzinie rzeczywistej

Przebieg zmienności funkcji

W matematyce na poziomie szkół średnich i w wielu praktycznych zastosowaniach rozpatruje się funkcje trygonometryczne dla argumentu będącego liczbą rzeczywistą. Mają one wówczas następujące własności:

Dziedzina i asymptoty

• Funkcje sinus i cosinus określone są dla każdej liczby rzeczywistej.
• Tangens jest określony w zbiorze powstałym ze zbioru wszystkich liczb rzeczywistych przez usunięcie liczb mających postać ${\tfrac {\pi }{2}}+k\pi ,$ gdzie $k$ jest liczbą całkowitą.
• Cotangens jest określony w zbiorze wszystkich liczb rzeczywistych poza liczbami postaci $k\pi ,$ gdzie $k$ jest liczbą całkowitą.
• Tangens i secans mają asymptoty pionowe w punktach postaci $x={\tfrac {\pi }{2}}+k\pi ,$ a cotangens i cosecans w punktach postaci $x=k\pi .$ Żadna z tych funkcji nie ma asymptot innego rodzaju.

Przeciwdziedzina

• Sinus i cosinus są ograniczone: przyjmują wartości z przedziału $[-1,1].$ Tangens i cotangens przyjmują dowolne wartości rzeczywiste, a secans i cosecans wartości ze zbioru $(-\infty ,-1]\cup [1,\infty ).$

Ekstrema

• Maksymalną wartość, dla obu funkcji $1,$ sinus przyjmuje w punktach $x={\tfrac {\pi }{2}}+2k\pi ,$ a cosinus w punktach $x=2k\pi ,$ gdzie $k$ jest liczbą całkowitą.
• Minimalną wartość, dla obu funkcji $-1,$ sinus przyjmuje w punktach $x=-{\tfrac {\pi }{2}}+2k\pi ,$ a cosinus w punktach $x=\pi +2k\pi ,$ gdzie $k$ jest liczbą całkowitą.

Miejsca zerowe

• Miejscami zerowymi sinusa i tangensa są punkty postaci $x=k\pi ,$ gdzie $k$ jest liczbą całkowitą.
• Miejscami zerowymi cosinusa i cotangensa są punkty postaci $x={\tfrac {\pi }{2}}+k\pi ,$ gdzie $k$ jest liczbą całkowitą.

Parzystość i nieparzystość

• Funkcje sinus, tangens, cotangens, cosecans są nieparzyste, a funkcje cosinus i secans parzyste:

  ${\begin{array}{l l}\sin(-x)=-\sin x&\cos(-x)=\cos x\\\operatorname {tg} (-x)=-\operatorname {tg} x&\operatorname {ctg} (-x)=-\operatorname {ctg} x\\\sec(-x)=\sec x&\operatorname {cosec} (-x)=-\operatorname {cosec} x\end{array}}$

Okresowość

• Funkcje trygonometryczne są funkcjami okresowymi. Okresem podstawowym sinusa, cosinusa, secansa i cosecansa jest liczba $2\pi ,$ a tangensa i cotangensa $\pi$:

  ${\begin{array}{l l}\sin x=\sin(x+2k\pi )&\cos x=\cos(x+2k\pi )\\\operatorname {tg} x=\operatorname {tg} (x+k\pi )&\operatorname {ctg} x=\operatorname {ctg} (x+k\pi )\\\sec x=\sec(x+2k\pi )&\operatorname {cosec} x=\operatorname {cosec} (x+2k\pi )\end{array}}$

gdzie $k$ jest liczbą całkowitą.

Ciągłość i różniczkowalność

• Funkcje sinus i cosinus są ciągłe i różniczkowalne w każdym punkcie prostej rzeczywistej. Tangens, cotangens, secans i cosecans także są ciągłe i różniczkowalne w swoich dziedzinach (zob. wyżej).

Odwracalność

• Żadna z nich nie jest różnowartościową, a zatem nie istnieją funkcje odwrotne do funkcji trygonometrycznych w całej dziedzinie. W pewnych przedziałach funkcje te są jednak różnowartościowe i można tam określić funkcje do nich odwrotne.

Własności algebraiczne

• Funkcje trygonometryczne zalicza się do funkcji elementarnych. Nie są one jednak funkcjami algebraicznymi.
• Liczby $\sin x$ oraz $\cos x$ są liczbami algebraicznymi dla dowolnych liczb postaci $x=r\pi ,$ gdzie $r$ jest liczbą wymierną.

Wykresy

Cosinusoida jest sinusoidą przesuniętą o wektor $\left[-{\tfrac {\pi }{2}},0\right].$ Szare linie pionowe na dolnych wykresach to asymptoty. Wykresy można powiększyć przez kliknięcie myszką.

• 
  Sinusoida: wykres funkcji $y=\sin x$
• 
  Cosinusoida: wykres funkcji $y=\cos x$

• 
  Tangensoida: wykres funkcji $y=\operatorname {tg} x$
• 
  Cotangensoida: wykres funkcji $y=\operatorname {ctg} x$

• 
  Wykres funkcji secans $y=\sec x={\frac {1}{\cos x}}$
• 
  Wykres funkcji cosecans $y=\operatorname {cosec} x={\frac {1}{\sin x}}$

Wartości dla typowych kątów

Wartości funkcji trygonometrycznych dla kątów 0°, 15°, 30°, 45°, 60°, 75°, 90°, 180°:

radiany	$0$	${\frac {\pi }{12}}$	${\frac {\pi }{6}}$	${\frac {\pi }{4}}$	${\frac {\pi }{3}}$	${\frac {5\pi }{12}}$	${\frac {\pi }{2}}$	$\pi$
stopnie	$0^{\circ }$	$15^{\circ }$	$30^{\circ }$	$45^{\circ }$	$60^{\circ }$	$75^{\circ }$	$90^{\circ }$	$180^{\circ }$
$\sin$	$0$	${\tfrac {{\sqrt {6}}-{\sqrt {2}}}{4}}$	${\tfrac {1}{2}}$	${\tfrac {\sqrt {2}}{2}}$	${\tfrac {\sqrt {3}}{2}}$	${\tfrac {{\sqrt {6}}+{\sqrt {2}}}{4}}$	$1$	$0$
$\cos$	$1$	${\tfrac {{\sqrt {6}}+{\sqrt {2}}}{4}}$	${\tfrac {\sqrt {3}}{2}}$	${\tfrac {\sqrt {2}}{2}}$	${\tfrac {1}{2}}$	${\tfrac {{\sqrt {6}}-{\sqrt {2}}}{4}}$	$0$	$-1$
$\operatorname {tg}$	$0$	$2-{\sqrt {3}}$	${\tfrac {\sqrt {3}}{3}}$	$1$	${\sqrt {3}}$	$2+{\sqrt {3}}$	nieokreślony	$0$
$\operatorname {ctg}$	nieokreślony	$2+{\sqrt {3}}$	${\sqrt {3}}$	$1$	${\tfrac {\sqrt {3}}{3}}$	$2-{\sqrt {3}}$	$0$	nieokreślony
$\sec$	$1$	${\sqrt {6}}-{\sqrt {2}}$	${\tfrac {2{\sqrt {3}}}{3}}$	${\sqrt {2}}$	$2$	${\sqrt {6}}+{\sqrt {2}}$	nieokreślony	$-1$
$\operatorname {cosec}$	nieokreślony	${\sqrt {6}}+{\sqrt {2}}$	$2$	${\sqrt {2}}$	${\tfrac {2{\sqrt {3}}}{3}}$	${\sqrt {6}}-{\sqrt {2}}$	$1$	nieokreślony

Wartości wszystkich funkcji trygonometrycznych dla argumentów postaci ${\tfrac {n\pi }{m}},n\in \mathbb {Z} ,m\in \mathbb {N_{+}}$ dają się zapisać za pomocą skończonego wzoru z użyciem podstawowych działań arytmetycznych i pierwiastka kwadratowego wtedy i tylko wtedy, gdy po skróceniu ułamka ${\tfrac {n}{m}}$ liczba $m$ jest iloczynem potęgi dwójki i różnych liczb pierwszych Fermata (jak dotąd znanych jest pięć takich liczb: 3, 5, 17, 257, 65537). W szczególności nie da się zapisać w ten sposób dokładnej wartości funkcji kąta 1°, gdyż $1^{\circ }={\tfrac {\pi }{180}},$ a $180=2^{2}\cdot 3^{2}\cdot 5$ ma drugą potęgę przy trójce. Warunek na $m$ jest identyczny jak warunek konstruowalności $m$-kąta foremnego za pomocą cyrkla i linijki (por. twierdzenie Gaussa-Wantzela).

Wzory redukcyjne

Wzory redukcyjne pozwalają sprowadzić dowolny rzeczywisty argument funkcji trygonometrycznej do argumentu z przedziału $[0,{\tfrac {\pi }{2}}),$ czyli $[0^{\circ },90^{\circ })$:

	I ćwiartka	II ćwiartka		III ćwiartka		IV ćwiartka
$\phi$	$90^{\circ }-\alpha$	$90^{\circ }+\alpha$	$180^{\circ }-\alpha$	$180^{\circ }+\alpha$	$270^{\circ }-\alpha$	$270^{\circ }+\alpha$	$360^{\circ }-\alpha$
	${\tfrac {\pi }{2}}-\alpha$	${\tfrac {\pi }{2}}+\alpha$	$\pi -\alpha$	$\pi +\alpha$	${\tfrac {3}{2}}\pi -\alpha$	${\tfrac {3}{2}}\pi +\alpha$	$2\pi -\alpha$
$\sin \phi$	$\cos \alpha$	$\cos \alpha$	$\sin \alpha$	$-\sin \alpha$	$-\cos \alpha$	$-\cos \alpha$	$-\sin \alpha$
$\cos \phi$	$\sin \alpha$	$-\sin \alpha$	$-\cos \alpha$	$-\cos \alpha$	$-\sin \alpha$	$\sin \alpha$	$\cos \alpha$
$\operatorname {tg} \phi$	$\operatorname {ctg} \alpha$	$-\operatorname {ctg} \alpha$	$-\operatorname {tg} \alpha$	$\operatorname {tg} \alpha$	$\operatorname {ctg} \alpha$	$-\operatorname {ctg} \alpha$	$-\operatorname {tg} \alpha$
$\operatorname {ctg} \phi$	$\operatorname {tg} \alpha$	$-\operatorname {tg} \alpha$	$-\operatorname {ctg} \alpha$	$\operatorname {ctg} \alpha$	$\operatorname {tg} \alpha$	$-\operatorname {tg} \alpha$	$-\operatorname {ctg} \alpha$
$\sec \phi$	$\operatorname {cosec} \alpha$	$-\operatorname {cosec} \alpha$	$-\sec \alpha$	$-\sec \alpha$	$-\operatorname {cosec} \alpha$	$\operatorname {cosec} \alpha$	$\sec \alpha$
$\operatorname {cosec} \phi$	$\sec \alpha$	$\sec \alpha$	$\operatorname {cosec} \alpha$	$-\operatorname {cosec} \alpha$	$-\sec \alpha$	$-\sec \alpha$	$-\operatorname {cosec} \alpha$

Aby zapamiętać zmianę funkcji, można wspomagać się następującą obserwacją: funkcja przechodzi w swoją kofunkcję, jeżeli rozpatrywany kąt ma postać $90^{\circ }\pm \alpha$ bądź $270^{\circ }\pm \alpha ,$ w przypadkach $0^{\circ }\pm \alpha =360^{\circ }\pm \alpha$ oraz $180^{\circ }\pm \alpha$ funkcja nie ulega zmianie. Znaki w poszczególnych ćwiartkach układu dla odpowiednich funkcji w powyższej tabelce zgodne są ze znakami redukowanych funkcji w danej ćwiartce według tabeli:

Ćwiartki układu współrzędnych

	I ćwiartka	II ćwiartka	III ćwiartka	IV ćwiartka
$\sin \alpha$	+	+	–	–
$\cos \alpha$	+	–	–	+
$\operatorname {tg} \alpha$	+	–	+	–
$\operatorname {ctg} \alpha$	+	–	+	–
$\sec \alpha$	+	–	–	+
$\operatorname {cosec} \alpha$	+	+	–	–

Metodą mnemotechniczną zapamiętania znaków dla stosowanych najczęściej w redukcji pierwszych czterech spośród powyższych funkcji jest popularny wierszyk nieznanego autora:

W pierwszej ćwiartce są dodatnie,

w drugiej tylko sinus,

w trzeciej tangens i cotangens,

a w czwartej cosinus.

W innych wersjach pierwszy wers brzmi:

W pierwszej ćwiartce same plusy lub W pierwszej wszystkie są dodatnie.

Podstawowe tożsamości trygonometryczne

Związki między funkcjami trygonometrycznymi spełnione dla dowolnego argumentu ich dziedziny to tzw. tożsamości trygonometryczne. Są one prawdziwe zarówno w dziedzinie rzeczywistej, jak i zespolonej. Często używane są:

• jedynka trygonometryczna:

$\sin ^{2}\alpha +\cos ^{2}\alpha =1$

• definicja tangensa i cotangensa za pomocą sinusa i cosinusa (pozwala wyprowadzić tożsamości dla tangensa i cotangensa z tożsamości dla sinusa i cosinusa):

${\begin{aligned}\operatorname {tg} \alpha &={\tfrac {\sin \alpha }{\cos \alpha }},\;\alpha \neq {\tfrac {\pi }{2}}+k\pi \\\operatorname {ctg} \alpha &={\tfrac {\cos \alpha }{\sin \alpha }},\;\alpha \neq k\pi \end{aligned}},\quad k\in \mathbb {Z} .$

Geometryczny dowód wzoru $\sin(\alpha +\beta )=\sin \alpha \cdot \cos \beta +\cos \alpha \cdot \sin \beta$

• wzory na sinus i cosinus sumy i różnicy kątów:

$\sin(\alpha \pm \beta )=\sin \alpha \cdot \cos \beta \pm \cos \alpha \cdot \sin \beta$

$\cos(\alpha \pm \beta )=\cos \alpha \cdot \cos \beta \mp \sin \alpha \cdot \sin \beta$

• wzory na sumę i różnicę sinusów i cosinusów:

$\sin \alpha \pm \sin \beta =2\sin {\tfrac {\alpha \pm \beta }{2}}\cdot \cos {\tfrac {\alpha \mp \beta }{2}}$

$\cos \alpha +\cos \beta =2\cos {\tfrac {\alpha +\beta }{2}}\cdot \cos {\tfrac {\alpha -\beta }{2}}$

$\cos \alpha -\cos \beta =-2\sin {\tfrac {\alpha +\beta }{2}}\cdot \sin {\tfrac {\alpha -\beta }{2}}$

• wzory na sinus i cosinus podwojonego argumentu:

$\sin 2\alpha =2\sin \alpha \cdot \cos \alpha$

$\cos 2\alpha =\cos ^{2}\alpha -\sin ^{2}\alpha =2\cos ^{2}\alpha -1=1-2\sin ^{2}\alpha$

• wzory na sinus i cosinus połowy argumentu:

$\left|\sin {\tfrac {1}{2}}\alpha \right|={\sqrt {\tfrac {1-cos\alpha }{2}}}$

$\left|\cos {\tfrac {1}{2}}\alpha \right|={\sqrt {\tfrac {1+cos\alpha }{2}}}$

• iloczyn w postaci sumy:

$\cos \alpha \cdot \cos \beta ={\tfrac {\cos(\alpha -\beta )+\cos(\alpha +\beta )}{2}}$

$\sin \alpha \cdot \sin \beta ={\tfrac {\cos(\alpha -\beta )-\cos(\alpha +\beta )}{2}}$

$\sin \alpha \cdot \cos \beta ={\tfrac {\sin(\alpha -\beta )+\sin(\alpha +\beta )}{2}}$

• wzory na wyrażanie jednych funkcji trygonometrycznych przez inne:

$\sin \alpha =\cos \left({\tfrac {\pi }{2}}-\alpha \right)$

$\cos \alpha =\sin \left({\tfrac {\pi }{2}}-\alpha \right)$

$\operatorname {tg} \alpha ={\tfrac {\sin \alpha }{\cos \alpha }}=\operatorname {ctg} \left({\tfrac {\pi }{2}}-\alpha \right)={\tfrac {1}{\operatorname {ctg} \alpha }}$

$\operatorname {ctg} \alpha ={\tfrac {\cos \alpha }{\sin \alpha }}=\operatorname {tg} \left({\tfrac {\pi }{2}}-\alpha \right)={\tfrac {1}{\operatorname {tg} \alpha }}$

$\sec \alpha ={\tfrac {1}{\cos \alpha }}=\operatorname {cosec} \left({\tfrac {\pi }{2}}-\alpha \right)$

$\operatorname {cosec} \alpha ={\tfrac {1}{\sin \alpha }}=\sec \left({\tfrac {\pi }{2}}-\alpha \right)$

${\begin{matrix}\color {red}{\sin ^{2}\alpha }=&1-\cos ^{2}\alpha =&{\tfrac {\operatorname {tg} ^{2}\alpha }{1+\operatorname {tg} ^{2}\alpha }}=&{\tfrac {1}{1+\operatorname {ctg} ^{2}\alpha }}\\1-\sin ^{2}\alpha =&\color {red}{\cos ^{2}\alpha }=&{\tfrac {1}{1+\operatorname {tg} ^{2}\alpha }}=&{\tfrac {\operatorname {ctg} ^{2}\alpha }{1+\operatorname {ctg} ^{2}\alpha }}\\{\tfrac {\sin ^{2}\alpha }{1-\sin ^{2}\alpha }}=&{\tfrac {1-\cos ^{2}\alpha }{\cos ^{2}\alpha }}=&\color {red}{\operatorname {tg} ^{2}\alpha }=&{\tfrac {1}{\operatorname {ctg} ^{2}\alpha }}\\{\tfrac {1-\sin ^{2}\alpha }{\sin ^{2}\alpha }}=&{\tfrac {\cos ^{2}\alpha }{1-\cos ^{2}\alpha }}=&{\tfrac {1}{\operatorname {tg} ^{2}\alpha }}=&\color {red}{\operatorname {ctg} ^{2}\alpha }\end{matrix}}$

(Zastrzeżenie formalne: Równości powyżej są prawdziwe tylko dla argumentów, dla których wszystkie użyte funkcje są określone, a w mianownikach nie występują zera)

Pochodne funkcji trygonometrycznych

Zachodzą równości:

$\sin 'x=\cos x=\sin \left({\tfrac {\pi }{2}}+x\right)$

$\cos 'x=-\sin x=\cos \left({\tfrac {\pi }{2}}+x\right)$

$\operatorname {tg} 'x={\tfrac {1}{\cos ^{2}x}}=\sec ^{2}x=1+\operatorname {tg} ^{2}x{\mbox{ dla }}x\neq {\tfrac {\pi }{2}}+k\pi ,k\in \mathbb {Z}$

$\operatorname {ctg} 'x=-{\tfrac {1}{\sin ^{2}x}}=-\operatorname {cosec} ^{2}x=-(1+\operatorname {ctg} ^{2}x){\mbox{ dla }}x\neq k\pi ,k\in \mathbb {Z}$

$\sec 'x={\tfrac {\sin x}{\cos ^{2}x}}=\operatorname {tg} x\sec x{\mbox{ dla }}x\neq {\tfrac {\pi }{2}}+k\pi ,k\in \mathbb {Z}$

$\operatorname {cosec} 'x=-{\tfrac {\cos x}{\sin ^{2}x}}=-\operatorname {ctg} x\operatorname {cosec} x{\mbox{ dla }}x\neq k\pi ,k\in \mathbb {Z}$

Można z nich otrzymać pochodne wyższych rzędów:

$\sin ^{(n)}x=\sin \left({\tfrac {n\pi }{2}}+x\right)={\begin{cases}\sin x&n=4k\\[2pt]\cos x&n=4k+1\\[2pt]-\sin x&n=4k+2\\[2pt]-\cos x&n=4k+3\end{cases}}{\mbox{ dla }}k\in \{0,1,2,\dots \},$

$\cos ^{(n)}x=\cos \left({\tfrac {n\pi }{2}}+x\right)={\begin{cases}\cos x&n=4k\\[2pt]-\sin x&n=4k+1\\[2pt]-\cos x&n=4k+2\\[2pt]\sin x&n=4k+3\end{cases}}{\mbox{ dla }}k\in \{0,1,2,\dots \}.$

Wzory na $n$-te pochodne pozostałych funkcji trygonometrycznych również istnieją, jednak są o wiele bardziej skomplikowane.

Całki funkcji trygonometrycznych

Podstawowe całki to:

$\int \sin x\mathrm {d} x=-\cos x+C,$

$\int \cos x\mathrm {d} x=\sin x+C,$

$\int \operatorname {tg} x\mathrm {d} x=-\ln |\cos x|+C,$

$\int \operatorname {ctg} x\mathrm {d} x=\ln |\sin x|+C,$

$\int \sec x\mathrm {d} x=\ln |\sec x+\operatorname {tg} x|+C,$

$\int \operatorname {cosec} x\mathrm {d} x=-\ln |\operatorname {cosec} x+\operatorname {ctg} x|+C,$

gdzie $C\in \mathbb {R} .$

Każda całka funkcji wymiernej postaci $R(\sin x,\cos x)$ jest elementarna, można ją obliczyć przez podstawienie:

$t=\operatorname {tg} {\tfrac {x}{2}},$

wówczas:

$\operatorname {d} x={\tfrac {2\operatorname {d} t}{1+t^{2}}},$

$\sin x={\tfrac {2t}{1+t^{2}}},$

$\cos x={\tfrac {1-t^{2}}{1+t^{2}}},$

$\operatorname {tg} x={\tfrac {2t}{1-t^{2}}},$

$\operatorname {ctg} x={\tfrac {1-t^{2}}{2t}},$

$\sec x={\tfrac {1+t^{2}}{1-t^{2}}},$

$\operatorname {cosec} x={\tfrac {1+t^{2}}{2t}}.$

Własności w dziedzinie zespolonej

Używając definicji analitycznych funkcji trygonometrycznych można te funkcje uogólnić m.in. na liczby zespolone.

Porównanie z funkcjami zmiennej rzeczywistej

Uogólnione w ten sposób funkcje trygonometryczne zachowują większość własności zmiennej rzeczywistej:

• okresowość (w tym okres podstawowy),
• tożsamości trygonometryczne,
• miejsca zerowe,
• punkty nieokreśloności:
  • sinus i cosinus są określone w całym zbiorze liczb zespolonych,
  • tangens jest określony w zbiorze liczb zespolonych, których usunięto liczby postaci ${\tfrac {(2k-1)\pi }{2}},$ a cotangens – punktów postaci $k\pi ,$ gdzie $k$ jest całkowita.

Zasadniczą różnicą jest brak ograniczoności funkcji sinus i cosinus. Przykładowo cosinus niezerowego argumentu urojonego jest zawsze liczbą rzeczywistą większą od $1,$ w szczególności:

$\cos i={\tfrac {1}{2}}(e^{-1}+e)\approx 1{,}543;\qquad \sin i={\tfrac {1}{2i}}(e^{-1}-e)\approx 1{,}175i$

Funkcje trygonometryczne zmiennej zespolonej są (nieskończenie) wielokrotne na całej płaszczyźnie zespolonej.

Części rzeczywiste, urojone, moduły i argumenty

Funkcja	Część rzeczywista	Część urojona	Moduł
$\sin(x\pm iy)$	$\sin x\cosh y$	$\pm \cos x\sinh y$	${\sqrt {\sin ^{2}x+\sinh ^{2}y}}$
$\cos(x\pm iy)$	$\cos x\cosh y$	$\mp \sin x\sinh y$	${\sqrt {\cos ^{2}x+\sinh ^{2}y}}$
$\operatorname {tg} (x\pm iy)$	${\frac {\sin 2x}{\cos 2x+\cosh 2y}}$	$\pm {\frac {\sinh 2y}{\cos 2x+\cosh 2y}}$	${\sqrt {\frac {\sin ^{2}2x+\sinh ^{2}2y}{(\cos 2x+\cosh 2y)^{2}}}}$
$\operatorname {ctg} (x\pm iy)$	$-{\frac {\sin 2x}{\cos 2x-\cosh 2y}}$	$\pm {\frac {\sinh 2y}{\cos 2x-\cosh 2y}}$	${\sqrt {-{\frac {\cos 2x+\cosh 2y}{\cos 2x-\cosh 2y}}}}$

Argument $\varphi$ oblicza się według wzorów:

$\sin \varphi ={\tfrac {\operatorname {Im} \omega }{|\omega |}},$

$\cos \varphi ={\tfrac {\operatorname {Re} \omega }{|\omega |}},$

gdzie $\omega$ to wartość odpowiedniej funkcji trygonometrycznej.

Wzór Eulera

W dziedzinie zespolonej zachodzi związek, zwany wzorem Eulera:

$e^{iz}=\cos z+i\sin z.$

Wynika z niego, iż:

$\sin z={\tfrac {e^{iz}-e^{-iz}}{2i}},$

$\cos z={\tfrac {e^{iz}+e^{-iz}}{2}},$

$\operatorname {tg} z={\tfrac {e^{iz}-e^{-iz}}{(e^{iz}+e^{-iz})i}},$

$\operatorname {ctg} z={\tfrac {e^{iz}+e^{-iz}}{e^{iz}-e^{-iz}}}i,$

$\sec z={\tfrac {2}{e^{iz}+e^{-iz}}},$

$\operatorname {cosec} z={\tfrac {2i}{e^{iz}-e^{-iz}}},$

gdzie:

• $e$ jest stałą, zwaną podstawą logarytmu naturalnego,
• $i$ jest jednostką urojoną $(i^{2}=-1).$

Wzory te pozwalają na niemal mechaniczne upraszczanie wyrażeń trygonometrycznych.

Wykresy

Liczby zespolone na płaszczyźnie zespolonej zostały oznaczone kolorami, zgodnie z umownym schematem. Odcienie barw określają argument, a jasność – moduł wyniku

• 
  Funkcja sinus
• 
  Funkcja cosinus
• 
  Funkcja tangens
• 
  Funkcja cotangens
• 
  Funkcja secans
• 
  Funkcja cosecans
• 
  Kod kolorów

Zastosowania matematyczne

Ze względu na obecność funkcji trygonometrycznych w najróżniejszych działach nauki i techniki nie jest możliwe podanie wszystkich ich zastosowań. Poniżej wymieniono więc tylko niektóre.

Geometria

Bezpośrednim zastosowaniem funkcji trygonometrycznych w geometrii elementarnej jest wyznaczanie długości boków lub kątów trójkąta. Poniżej podano kilka innych zastosowań.

Twierdzenia sinusów, cosinusów i tangensów

Oznaczenia

Geometryczny dowód twierdzenia cosinusów dla kątów ostrych. Obydwie figury mają równe pola powierzchni.

W każdym trójkącie (przy oznaczeniach standardowych, zob. rysunek) zachodzą następujące równości:

Twierdzenie sinusów, inaczej twierdzenie Snelliusa:

${\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}=2R$

($R$ jest promieniem okręgu opisanego)

Twierdzenie cosinusów, inaczej twierdzenie Carnota:

$c^{2}=a^{2}+b^{2}-2ab\cos \gamma$

Twierdzenie tangensów, inaczej twierdzenie Regiomontana:

${\frac {a-b}{a+b}}={\frac {\operatorname {tg} {\frac {\alpha -\beta }{2}}}{\operatorname {tg} {\frac {\alpha +\beta }{2}}}}.$

W geometrii sferycznej istnieje także twierdzenie haversinów, związane z nieużywaną dziś funkcją trygonometryczną $\operatorname {haversin} x=1-\cos {\tfrac {x}{2}},$ pozwalające na obliczanie odległości pomiędzy dwoma punktami na sferze.

Wzory na pole trójkąta

Wzory na pole trójkąta często wykorzystują funkcje trygonometryczne:

$S={\frac {bc\sin \alpha }{2}}$

lub

$S=2R^{2}\sin \alpha \sin \beta \sin \gamma$

lub

$S={\frac {a^{2}+b^{2}+c^{2}}{4(\operatorname {ctg} \alpha +\operatorname {ctg} \beta +\operatorname {ctg} \gamma )}},$

gdzie:

• $a,b,c$ to boki trójkąta,
• $\alpha ,\beta ,\gamma$ to miary kątów o wierzchołkach leżących naprzeciw boków odpowiednio $a,b$ i $c,$
• $R$ to promień koła opisanego.

Iloczyny wektorów

W geometrii i algebrze liniowej definiowane są iloczyny wektorów, m.in. iloczyny skalarny i wektorowy. Czasem konieczne jest obliczenie wartości iloczynu skalarnego lub wektorowego dla wektorów o znanych kierunkach, zwrotach i długościach. Wzory wykorzystują funkcje trygonometryczne kąta $\theta$ między wektorami:

• iloczyn skalarny,

  ${\vec {a}}\cdot {\vec {b}}=|{\vec {a}}|\,|{\vec {b}}|\cos \theta ,$

• iloczyn wektorowy,

  ${\vec {a}}\times {\vec {b}}=(|{\vec {a}}|\,|{\vec {b}}|\sin \theta )\,{\vec {n}},$

gdzie ${\vec {n}}$ jest ustalonym wektorem jednostkowym prostopadłym tak do ${\vec {a}},$ jak i do ${\vec {b}}.$

Współrzędne biegunowe, sferyczne i walcowe

Najczęściej w geometrii stosowany jest układ współrzędnych kartezjańskich. Niekiedy jednak wygodnie jest stosować inne układy, w których niektóre współrzędne są wyznaczone za pomocą kątów. Do takich układów należy układ współrzędnych biegunowych, układ współrzędnych sferycznych (jego zastosowaniem są np. współrzędne geograficzne) i układ współrzędnych walcowych. Wówczas przydatne są funkcje trygonometryczne, m.in. do przeliczania takich współrzędnych na współrzędne kartezjańskie.

Geometria sferyczna

Funkcje trygonometryczne są ważnymi narzędziami geometrii sferycznej i jej zastosowań w astronomii, nawigacji i geodezji, gdzie służą m.in. do rozwiązywania trójkątów sferycznych.

Analiza matematyczna

Szereg Fouriera

Przedstawienie fali prostokątnej w postaci szeregu harmonicznych

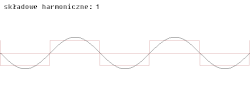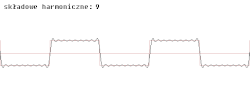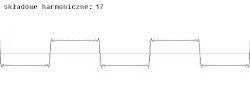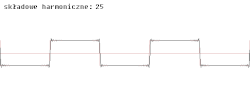
Funkcje $\left\{{\tfrac {1}{\sqrt {2\pi }}},{\tfrac {\sin nx}{\sqrt {\pi }}},{\tfrac {\cos nx}{\sqrt {\pi }}}\right\}$ tworzą dla dowolnego $n\in \mathbb {N} _{+}$ układ ortonormalny. Dzięki temu funkcje okresowe $S(x)$ spełniające warunki Dirichleta mogą być wyrażone w postaci szeregu Fouriera:

$S(x)={\tfrac {1}{2}}a_{0}+\sum _{n=1}^{\infty }\left(a_{n}\cos {\tfrac {2n\pi }{T}}x+b_{n}\sin {\tfrac {2n\pi }{T}}x\right).$

Można go również wyrazić za pomocą np. samych funkcji sinus. Poszczególne składowe tego szeregu nazywane są harmonicznymi. Szereg Fouriera odgrywa wielką rolę w fizyce, teorii drgań, a nawet teorii muzyki (zob. szereg harmoniczny (muzyka), alikwoty).

Funkcja Weierstrassa

Funkcja Weierstrassa

Za pomocą szeregu trygonometrycznego definiowana jest funkcja Weierstrassa, która jest ciągła, jednak nie jest w żadnym punkcie różniczkowalna:

$f(x)=\sum _{n=0}^{\infty }a^{n}\cos(b^{n}\pi x),$

gdzie $a$ jest pewną liczbą z przedziału $(0,1)$ natomiast $b$ jest liczbą nieparzystą, spełniającą warunek $ab>1+{\tfrac {3}{2}}\pi .$

Funkcja Dirichleta

Za pomocą funkcji cosinus definiowana jest tzw. funkcja Dirichleta, która przyjmuje wartość 1 dla argumentów wymiernych i 0 dla niewymiernych:

$1_{\mathbb {Q} }(x)=\lim _{m\to \infty }\lim _{n\to \infty }\cos ^{2n}(m!\pi x).$

Teoria liczb

Funkcja Möbiusa $\mu (n)$ może być wyrażona trygonometrycznie:

$\mu (n)=\sum _{\begin{smallmatrix}1\leqslant x<n,\\\operatorname {NWD} (x,n)=1\end{smallmatrix}}\!\!\!\!\!\!\!\!\cos {\tfrac {2\pi x}{n}}.$

Zastosowania poza matematyką

Funkcje trygonometryczne znalazły zastosowania w różnych naukach ścisłych, w tym na pograniczu tych nauk z humanistyką i sztuką.

Nauki przyrodnicze

Krzywe Lissajous powstają przez złożenie sinusoidalnych drgań o różnej częstotliwości w pionie i w poziomie

• akustyka: np. analiza harmoniczna,
• astronomia, nawigacja, kartografia, oceanografia: trygonometria sferyczna stosowana do powierzchni Ziemi
• astronomia i geodezja: paralaksa pozwala wyznaczać odległości bez przebywania ich, nawet tysięcy lat świetlnych.
• chemia i krystalografia: obliczanie odległości pomiędzy atomami w krysztale,
• fizyka: np. ruch harmoniczny, prawo załamania światła, zob. też sekcję Harmoniki tego artykułu,
• geofizyka, sejsmologia: badanie fal sejsmicznych,
• optyka: prawo załamania światła, polaryzacja fali,
• teoria chaosu.

Nauki społeczne

• ekonomia (w szczególności analiza rynków finansowych), probabilistyka, statystyka, meteorologia: np. analiza harmoniczna szeregów czasowych
• fonetyka, analiza języka naturalnego: analiza harmoniczna głosek
• teoria muzyki: np. alikwoty, szereg harmoniczny.

Nauki techniczne

• architektura, mechanika: bezpośrednie zastosowanie do elementów trójkąta
• elektryka i elektronika: np. przebiegi sinusoidalne prądu zmiennego
• geodezja, inżynieria lądowa: w szczególności niwelacja trygonometryczna,
• grafika komputerowa: np. symulowanie odbicia i załamania światła w ray tracingu
• kompresja obrazu: np. przy kompresji JPEG
• kryptologia: w związku z zastosowaniami w teorii liczb,
• obrazowanie medyczne: tomografia komputerowa i USG wymagają obliczeń trygonometrycznych
• robotyka: np. algorytm sterowania sinusoidalnego.

Polskie nazwy

Poloniści dopuszczają zarówno formy „cosinus, cotangens, cosecans, secans”, jak i „kosinus, kotangens, kosekans, sekans”. Słowniki języka polskiego skłaniają się ku tym drugim jako bardziej naturalnym dla języka polskiego, jednak słowniki i encyklopedie matematyczne raczej nie używają form spolszczonych, podobnie w naukowej literaturze matematycznej są one rzadko spotykane.

Już pod koniec XVIII wieku Jan Śniadecki próbował wprowadzić całkowicie polskie odpowiedniki nazw i skrótów funkcji trygonometrycznych (w nawiasie proponowany skrót):

• sinus – wstawa (wst),
• cosinus – dostawa (dost),
• tangens – styczna (sty),
• cotangens – dostyczna (dosty),
• secans – sieczna (sie),
• cosecans – dosieczna (dosie).

Propagowali je potem m.in.:

• Andrzej Radwański w dziele „Słownik wyrazów grecko-łacińskich w poznawaniu Rody używanych… bezpłatnie dodany do dzieła Treść nauki przyrodzenia” wydanym w 1850 roku. Zwalczał tam wszelkie nazwy pochodzące z greki i łaciny;
• prof. Maksymilian Thullie (1853–1939), rektor Szkoły Politechnicznej we Lwowie. W latach 1918–1924 próbował forsować polskie nazwy w swoich pracach, np. w podręczniku Statyka budowli (wyd. IV, Lwów 1921), jednak nie przyjęły się.

Oznaczenia

W różnych językach stosuje się różne skróty funkcji trygonometrycznych. Oznaczenia kosinusa są jednakowe we wszystkich podanych, a sekansa i kosekansa – jednakowe prawie wszędzie, poza językiem francuskim, gdzie nad tymi skrótami zdarza się akcent: séc, coséc. Różnice w skrótach pozostałych trzech funkcji przedstawia poniższa tabela:

język	sinus	tangens	cotangens
angielski	sin	tan, tg	cot, ctg, ctn
chiński	sin	tan, tg	cot, ctg
fiński	sin	tan	cot
francuski	sin	tan, tang, tg	cotan, cotg, cot, ctg
hiszpański	sen	tan, tg, tag	cot, cotg, ctg
niderlandzki	sin	tan	cot
indonezyjski	sin	tan	cot
japoński	sin	tan	cot
koreański	sin	tan	cot
litewski	sin	tg	ctg
niemiecki	sin	tan, tg	cot, ctg
portugalski	sen, sin	tan, tg	cot, ctg
rosyjski	sin	tg	ctg
turecki	sin	tan	cot
ukraiński	sin	tg	ctg
węgierski	sin	tg	ctg
włoski	sen, sin	tan, tg	cot, ctg

Związki z innymi funkcjami

Funkcjami trygonometrycznymi definiuje się inne pojęcia matematyczne, np.:

• inne funkcje elementarne jak harmoniki, funkcje kołowe i funkcja sinc;
• niektóre funkcje specjalne jak sinus całkowy i cosinus całkowy, całki Fresnela, funkcje sferyczne i kuliste;
• inne funkcje rzeczywiste jak funkcja Weierstrassa;
• krzywe będące wykresami tych funkcji w dziedzinie rzeczywistej; dla sinusa, kosinusa, tangensa i kotangensa te krzywe to odpowiednio sinusoida, kosinusoida, tangensoida i kotangensoida;
• inne krzywe jak sinusoida zagęszczona.

Do funkcji trygonometrycznych nawiązuje też nazewnictwo niektórych innych funkcji:

• elementarnych jak funkcje hiperboliczne, mające analogiczne własności, oraz odwrotne do nich funkcje polowe;
• specjalnych jak całkowy sinus hiperboliczny.

Funkcje odwrotne do trygonometrycznych

Funkcje odwrotne do trygonometrycznych nazywane są też funkcjami kołowymi lub cyklometrycznymi. Ze względu na okresowość funkcji trygonometrycznych funkcje te są do nich odwrotne jedynie w przedziale obejmującym jeden okres.

Nazwa	Zapis	Odwrotna do	Dziedzina	Przeciwdziedzina
arcus sinus	$y=\arcsin x$	$x=\sin y$	$[-1,1]$	$[-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}]$
arcus cosinus	$y=\arccos x$	$x=\cos y$	$[-1,1]$	$[0,\pi ]$
arcus tangens	$y=\operatorname {arctg} x$	$x=\operatorname {tg} y$	$\mathbb {R}$	$(-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}})$
arcus cotangens	$y=\operatorname {arcctg} x$	$x=\operatorname {ctg} y$	$\mathbb {R}$	$(0,\pi )$
arcus secans	$y=\operatorname {arcsec} x$	$x=\sec y$	$\mathbb {R} \setminus (-1,1)$	$[0,{\tfrac {\pi }{2}})\cup ({\tfrac {\pi }{2}},\pi ]$
arcus cosecans	$y=\operatorname {arccosec} x$	$x=\operatorname {cosec} y$	$\mathbb {R} \setminus (-1,1)$	$[-{\tfrac {\pi }{2}},0)\cup (0,{\tfrac {\pi }{2}}]$

Harmoniki

Sinusoidalny ruch prostego oscylatora

Funkcje postaci

$u(t)=A\sin(\omega t+\phi ),$

gdzie:

• $A$ – amplituda,
• $\omega$ – prędkość kątowa (pulsacja),
• $\phi$ – faza początkowa

są nazywane harmonikami. Funkcje sinus i cosinus są ich szczególnymi przypadkami. Harmoniki mają duże znaczenie w praktyce, przy analizie funkcji okresowych. Kombinacja liniowa kilku harmonik o tej samej częstotliwości jest ciągle harmoniką o tej częstotliwości.

Harmoniki stosowane są w fizyce przy badaniu wszelkich zjawisk okresowych, np. drgań. Wiele z tych zjawisk, np. masa na sprężynie, wahadło przy niewielkim wychyleniu albo elektryczny obwód rezonansowy, w wyidealizowanym przypadku (przy braku strat energii), opisuje równanie różniczkowe:

$x''=-kx,$

którego rozwiązaniami są harmoniki.

Funkcje hiperboliczne

Sinus, cosinus i tangens hiperboliczny

Jak podano w sekcji Definicja za pomocą równań funkcyjnych, funkcje sinus i cosinus można zdefiniować w następujący sposób:

$\left\{{\begin{matrix}W1\colon &s(x_{1}-x_{2})=s(x_{1})c(x_{2})-c(x_{1})s(x_{2})\\W2\colon &c(x_{1}-x_{2})=c(x_{1})c(x_{2})+s(x_{1})s(x_{2})\\W3\colon &\lim _{x\to 0}{\tfrac {s(x)}{x}}=1\end{matrix}}\right.$

Jeśli warunek W2 zmienić na:

$W2'\colon \quad c(x_{1}-x_{2})=c(x_{1})c(x_{2})-s(x_{1})s(x_{2}),$

wówczas warunki W1, W2', W3 będą spełnione przez inne funkcje, które przez analogię nazywane są sinusem hiperbolicznym (sinh) i cosinusem hiperbolicznym (cosh).

Analogicznie jak dla funkcji trygonometrycznych definiuje się też tangens, cotangens, secans i cosecans hiperboliczny jako odpowiednie ilorazy z udziałem sinusa i cosinusa hiperbolicznego. Istnieje także całkowy sinus hiperboliczny i całkowy cosinus hiperboliczny.

Pole zakreskowanego obszaru odpowiada połowie argumentu funkcji hiperbolicznych

Pole zakreskowanego obszaru odpowiada połowie argumentu funkcji trygonometrycznych

Także definicja na okręgu jednostkowym dla funkcji trygonometrycznych ma swój odpowiednik hiperboliczny. Zamiast okręgu jednostkowego

$x^{2}+y^{2}=1$

należy wziąć hiperbolę o równaniu

$x^{2}-y^{2}=1.$

Na okręgu jednostkowym argument funkcji trygonometrycznych odpowiadał mierze kąta, jednak jest ona równa polu wycinka kołowego, symetrycznego względem osi OX. Podobnie w przypadku funkcji hiperbolicznych argumentowi odpowiada pole odpowiedniego wycinka. Biorąc długości odcinków, które na okręgu odpowiadały funkcjom sinus, cosinus i tangens, uzyskuje się na hiperboli sinus, cosinus i tangens hiperboliczny.

Istnieją też inne analogie. Dla funkcji trygonometrycznych zachodzą równości, podane w sekcji Wzór Eulera.

Analogiczne wzory występują dla funkcji hiperbolicznych:

${\begin{aligned}\sinh x&={\tfrac {e^{x}-e^{-x}}{2}}\\\cosh x&={\tfrac {e^{x}+e^{-x}}{2}}\\\operatorname {tgh} x&={\tfrac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}\\\operatorname {ctgh} x&={\tfrac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}\end{aligned}}$

Istnieją też analogie niektórych tożsamości trygonometrycznych:

$\sinh(x+y)=\sinh x\cosh y+\cosh x\sinh y$

$\cosh ^{2}x-\sinh ^{2}x=1$

$\cosh 2x=\cosh ^{2}x+\sinh ^{2}x$

Podobieństwa te wynikają z głębokiej symetrii pomiędzy funkcjami trygonometrycznymi a hiperbolicznymi, przejawiającej się także po ich uogólnieniu na argumenty zespolone.

Zobacz też

• cosinusy kierunkowe
• kąt między dwiema krzywymi
• sinusoida Krzyżanowskiego

Bibliografia

• Igor N. Bronsztejn, Konstantin A. Siemiendiajew: Matematyka, poradnik encyklopedyczny. Wyd. VI. Warszawa: PWN, 1976.
• Lidia Filist, Artur Malina, Alicja Solecka: Słownik encyklopedyczny – matematyka. Wydawnictwo Europa, 1998. ISBN 83-85336-06-0.brak strony w książce
• Franciszek Leja: Funkcje zespolone. Warszawa: PWN, 1976.brak strony w książce
• Franciszek Leja: Rachunek różniczkowy i całkowy ze wstępem do równań różniczkowych. Wyd. III. Warszawa: PWN, 1954.brak strony w książce
• Fritz Reinhardt, Heinrich Soeder: Atlas matematyki. Warszawa: Prószyński i S-ka, 2006. ISBN 83-7469-189-1.

Linki zewnętrzne

• JarosławJ. Górnicki JarosławJ., Sinus i cosinus w akcji, [w:] pismo „Delta”, deltami.edu.pl, luty 2022, ISSN 0137-3005 [dostęp 2023-12-10]  (pol.).